4 by 4 matrix. Extends Mat with 4D-specific functionality and constructors. More...

#include <easy3d/core/mat.h>

Inheritance diagram for Mat4< T >:

Public Member Functions
	Mat4 ()=default
	Default constructor.

	Mat4 (T s)
	Constructor that initializes diagonal elements to a scalar value and others zeros.

	Mat4 (const Mat< 4, 4, T > &rhs)
	Copy constructor. This provides compatibility with generic operations implemented by Mat.

	Mat4 (T s00, T s01, T s02, T s03, T s10, T s11, T s12, T s13, T s20, T s21, T s22, T s23, T s30, T s31, T s32, T s33)
	Initialize elements from individual scalars. The digits following s in the parameter names indicate the row/column of the element being set.

	Mat4 (const T *m)
	Initialize elements from an array of type T.

	Mat4 (const Vec< 4, T > &x, const Vec< 4, T > &y, const Vec< 4, T > &z, const Vec< 4, T > &w)
	Initialize elements from four vectors. If MATRIX_ROW_MAJOR is defined, x, y, z and w specify rows of the matrix, else columns.

	Mat4 (const Mat< 3, 3, T > &rhs)
	Initialize from a 3D matrix. rhs forms the upper-left 3x3 sub-matrix, other elements are initialized as the identity.

	Mat4 (const Vec< 3, T > &s, const Quat< T > &r, const Vec< 3, T > &t)
	Initialize from scale/rotation/translation. The order of the transformations is scale, rotation, translation.

Mat3< T >	sub () const
	Return the upper-left 3x3 sub-matrix.

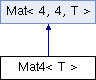
Public Member Functions inherited from Mat< 4, 4, T >
	Mat ()=default
	Default constructor.

	Mat (T s)
	Constructs a matrix with diagonal elements set to `s` and other elements set to zero.

	Mat (const Mat< rN, rM, T > &rhs)
	Copy constructor for matrices with different dimensions (rN >= N, rM >= M).

	Mat (const T *m)
	Constructs a matrix from an array of elements.

Vec< M, T >	row (size_t row) const
	Returns the specified row as a vector.

Vec< N, T >	col (size_t col) const
	Returns the specified column as a vector.

const T &	operator() (size_t row, size_t col) const
	Returns a constant reference to the element at the specified row and column.

T &	operator() (size_t row, size_t col)
	Returns a reference to the element at the specified row and column.

	operator const T * () const
	Returns a constant pointer to the matrix elements.

	operator T* ()
	Returns a pointer to the matrix elements.

void	load_zero ()
	Sets all elements to zero.

void	load_identity (T s=T(1))
	Sets the diagonal elements to `s` and other elements to zero.

void	set_row (size_t row, const Vec< vN, T > &v)
	Sets the specified row from a vector.

void	set_col (size_t col, const Vec< vN, T > &v)
	Sets the specified column from a vector.

void	swap_rows (size_t a, size_t b)
	Swaps the specified rows.

void	swap_cols (size_t a, size_t b)
	Swaps the specified columns.

bool	operator== (const Mat< N, M, T > &rhs) const
	Checks if the matrix is equal to another matrix.

bool	operator!= (const Mat< N, M, T > &rhs) const
	Checks if the matrix is not equal to another matrix.

Mat< N, rM, T >	operator* (const Mat< M, rM, T > &rhs) const
	Multiplies the matrix by another matrix.

Vec< N, T >	operator* (const Vec< M, T > &rhs) const
	Multiplies the matrix by a vector.

Mat< N, M, T >	operator* (T rhs) const
	Multiplies the matrix by a scalar.

Mat< N, M, T >	operator+ (const Mat< N, M, T > &rhs) const
	Adds the matrix to another matrix. Component-wise matrix-matrix addition.

Mat< N, M, T >	operator- (const Mat< N, M, T > &rhs) const
	Subtracts another matrix from the matrix. Component-wise matrix-matrix subtraction.

Mat< N, M, T >	operator- () const
	Negates the matrix. Component-wise matrix negation.

Mat< N, M, T >	operator/ (T rhs) const
	Divides the matrix by a scalar.

Mat< N, M, T > &	operator*= (const Mat< N, M, T > &rhs)
	Multiplies the matrix by another matrix and assigns the result to the matrix.

Mat< N, M, T > &	operator*= (T rhs)
	Multiplies the matrix by a scalar and assigns the result to the matrix.

Mat< N, M, T > &	operator+= (const Mat< N, M, T > &rhs)
	Adds another matrix to the matrix and assigns the result to the matrix.

Mat< N, M, T > &	operator+= (T rhs)
	Adds a scalar to the matrix and assigns the result to the matrix.

Mat< N, M, T > &	operator-= (const Mat< N, M, T > &rhs)
	Subtracts another matrix from the matrix and assigns the result to the matrix.

Mat< N, M, T > &	operator-= (T rhs)
	Subtracts a scalar from the matrix and assigns the result to the matrix.

Mat< N, M, T > &	operator/= (T rhs)
	Divides the matrix by a scalar and assigns the result to the matrix.

Static Public Member Functions
static Mat4< T >	scale (T s)
	Static constructor returning a 4D uniform scale matrix.

static Mat4< T >	scale (const Vec< 4, T > &s)
	Static constructor returning a 4D non-uniform scale matrix,.

static Mat4< T >	scale (T x, T y, T z, T w)
	Static constructor returning a 4D non-uniform scale matrix,.

static Mat4< T >	rotation (const Vec< 3, T > &axis, T angle)
	Static constructor returning a 3D rotation matrix defined by its axis and angle.

static Mat4< T >	rotation (const Vec< 3, T > &axis_angle)
	Static constructor returning a 3D rotation matrix defined by the axis–angle representation. Both the axis and the angle are represented by a vector codirectional with the rotation axis whose length is the rotation angle.

static Mat4< T >	rotation (const Quat< T > &q)
	Static constructor returning a 3D rotation matrix defined by a quaternion.

static Mat4< T >	rotation (T x, T y, T z, int order=312)
	Static constructor returning a 3D rotation matrix defined by Euler angles. The three rotations are applied successively.

static Mat4< T >	translation (const Vec< 3, T > &t)
	Static constructor return a 3D translation matrix (as a 4D affine transformation).

static Mat4< T >	translation (T x, T y, T z)
	Static constructor return a 3D translation matrix (as a 4D affine transformation).

Static Public Member Functions inherited from Mat< 4, 4, T >
static Mat< N, M, T >	identity ()
	Returns an identity matrix.

static size_t	num_rows ()
	Returns the number of rows in the matrix.

static size_t	num_columns ()
	Returns the number of columns in the matrix.

Detailed Description

template<typename T>
class easy3d::Mat4< T >

4 by 4 matrix. Extends Mat with 4D-specific functionality and constructors.

Template Parameters

T	The scalar type for vector elements.

See also: Mat.

Constructor & Destructor Documentation

◆ Mat4() [1/2]

template<typename T>

Mat4 ( )

default

Default constructor.

Note: The matrix elements are intentionally not initialized. This is efficient if the user assigns their values from subsequent computations. Use Mat4(T s) to initialize the elements during construction.

◆ Mat4() [2/2]

template<typename T>

Mat4 ( T s )

explicit

Constructor that initializes diagonal elements to a scalar value and others zeros.

Parameters

s	The scalar value to initialize the diagonal elements.

Member Function Documentation

◆ rotation() [1/4]

template<typename T>

Mat4< T > rotation ( const Quat< T > & q )

static

Static constructor returning a 3D rotation matrix defined by a quaternion.

Note: q is a unit quaternion representing a rotation.

◆ rotation() [2/4]

template<typename T>

Mat4< T > rotation	(	const Vec< 3, T > &	axis,
		T	angle )

static

Static constructor returning a 3D rotation matrix defined by its axis and angle.

Parameters

axis	Axis of rotation. This MUST be normalized.
angle	Angle of rotation in radians. Positive values of angle rotate counter-clockwise about axis as per the right-hand rule.

Note: The axis defines only the direction of the rotation axis, i.e., the rotation is about the axis passing through the origin.

◆ rotation() [3/4]

template<typename T>

Mat4< T > rotation ( const Vec< 3, T > & axis_angle )

static

Static constructor returning a 3D rotation matrix defined by the axis–angle representation. Both the axis and the angle are represented by a vector codirectional with the rotation axis whose length is the rotation angle.

Parameters

axis_angle direction is the axis and length is the angle (in radian)

Note: The axis defines only the direction of the rotation axis, i.e., the rotation is about the axis passing through the origin.

◆ rotation() [4/4]

template<typename T>

Mat4< T > rotation	(	T	x,
		T	y,
		T	z,
		int	order = 312 )

static

Static constructor returning a 3D rotation matrix defined by Euler angles. The three rotations are applied successively.

Parameters

x,y,z	the rotation angles (in radians) around X, Y, and Z axes respectively.
order	the order of the rotations to be applied. 1 first and 3 for last.

Note: Using a different order yields different results. The default order is first Y, then Z, then X. See http://www.opengl-tutorial.org/intermediate-tutorials/tutorial-17-quaternions/

◆ scale() [1/3]

template<typename T>

Mat4< T > scale ( const Vec< 4, T > & s )

static

Static constructor returning a 4D non-uniform scale matrix,.

Parameters

s	a 4D vector denoting the x, y, z, and w scales.

See also: scale(T s), scale(T x, T y, T z, T w).

◆ scale() [2/3]

template<typename T>

Mat4< T > scale ( T s )

static

Static constructor returning a 4D uniform scale matrix.

Parameters

s	x, y, z, w scale (uniform).

See also: scale(Vec<4, T> s), scale(T x, T y, T z, T w).

◆ scale() [3/3]

template<typename T>

Mat4< T > scale	(	T	x,
		T	y,
		T	z,
		T	w )

static

Static constructor returning a 4D non-uniform scale matrix,.

Parameters

x	x scale.
y	y scale.
z	z scale.
w	w scale.

See also: scale(T s), scale(Vec<4, T> s).

◆ translation() [1/2]

template<typename T>

Mat4< T > translation ( const Vec< 3, T > & t )

static

Static constructor return a 3D translation matrix (as a 4D affine transformation).

Parameters

t	Translation vector.

◆ translation() [2/2]

template<typename T>

Mat4< T > translation	(	T	x,
		T	y,
		T	z )

static

Static constructor return a 3D translation matrix (as a 4D affine transformation).

Parameters

x	The x component of the translation vector.
y	The y component of the translation vector.
z	The z component of the translation vector.

The documentation for this class was generated from the following file:

G:/3_code/Easy3D/easy3d/core/mat.h

Public Member Functions

Static Public Member Functions

Detailed Description

Constructor & Destructor Documentation

◆ Mat4() [1/2]

◆ Mat4() [2/2]

Member Function Documentation

◆ rotation() [1/4]

◆ rotation() [2/4]

◆ rotation() [3/4]

◆ rotation() [4/4]

◆ scale() [1/3]

◆ scale() [2/3]

◆ scale() [3/3]

◆ translation() [1/2]

◆ translation() [2/2]