|
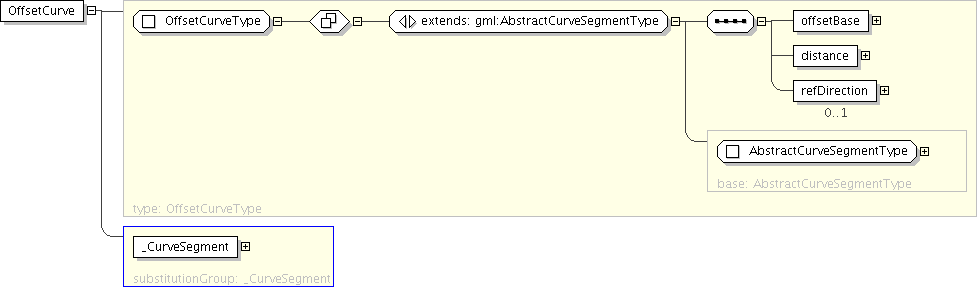
| Name | OffsetCurve |
|---|---|
| Type | gml:OffsetCurveType |
| Nillable | no |
| Abstract | no |

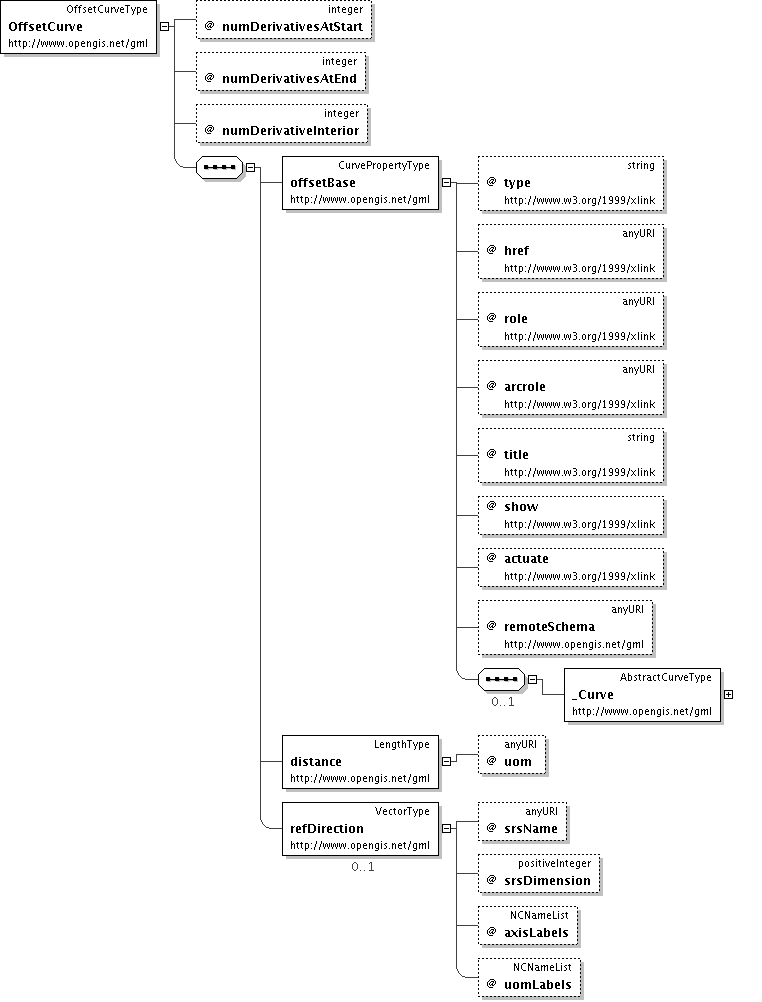
'The attribute \"numDerivativesAtStart\" specifies the type of continuity between this curve segment and its predecessor. If this is the first curve segment in the curve, one of these values, as appropriate, is ignored. The default value of \"0\" means simple continuity, which is a mandatory minimum level of continuity. This level is referred to as \"C 0 \" in mathematical texts. A value of 1 means that the function and its first derivative are continuous at the appropriate end point: \"C 1 \" continuity. A value of \"n\" for any integer means the function and its first n derivatives are continuous: \"C n \" continuity. NOTE: Use of these values is only appropriate when the basic curve definition is an underdetermined system. For example, line string segments cannot support continuity above C 0 , since there is no spare control parameter to adjust the incoming angle at the end points of the segment. Spline functions on the other hand often have extra degrees of freedom on end segments that allow them to adjust the values of the derivatives to support C 1 or higher continuity.'
"'The attribute \"numDerivativesAtEnd\" specifies the type of continuity between this curve segment and its successor. If this is the last curve segment in the curve, one of these values, as appropriate, is ignored. The default value of \"0\" means simple continuity, which is a mandatory minimum level of continuity. This level is referred to as \"C 0 \" in mathematical texts. A value of 1 means that the function and its first derivative are continuous at the appropriate end point: \"C 1 \" continuity. A value of \"n\" for any integer means the function and its first n derivatives are continuous: \"C n \" continuity. NOTE: Use of these values is only appropriate when the basic curve definition is an underdetermined system. For example, line string segments cannot support continuity above C 0 , since there is no spare control parameter to adjust the incoming angle at the end points of the segment. Spline functions on the other hand often have extra degrees of freedom on end segments that allow them to adjust the values of the derivatives to support C 1 or higher continuity.'
"'The attribute \"numDerivativesInterior\" specifies the type of continuity that is guaranteed interior to the curve. The default value of \"0\" means simple continuity, which is a mandatory minimum level of continuity. This level is referred to as \"C 0 \" in mathematical texts. A value of 1 means that the function and its first derivative are continuous at the appropriate end point: \"C 1 \" continuity. A value of \"n\" for any integer means the function and its first n derivatives are continuous: \"C n \" continuity. NOTE: Use of these values is only appropriate when the basic curve definition is an underdetermined system. For example, line string segments cannot support continuity above C 0 , since there is no spare control parameter to adjust the incoming angle at the end points of the segment. Spline functions on the other hand often have extra degrees of freedom on end segments that allow them to adjust the values of the derivatives to support C 1 or higher continuity.'
">'offsetBase is a reference to thecurve from which this curve is define as an offset.'
'distance is the distance at which the offset curve is generated from the basis curve. In 2D systems, positive distances are to be to the left of the basis curve, and the negative distances are to be to the right of the basis curve.'
'refDistance is used to define the vector direction of the offset curve from the basis curve. It can be omitted in the 2D case, where the distance can be positive or negative. In that case, distance defines left side (positive distance) or right side (negative distance) with respect to the tangent to the basis curve. In 3D the basis curve shall have a well defined tangent direction for every point. The offset curve at any point in 3D, the basis curve shall have a well-defined tangent direction for every point. The offset curve at any point (parameter) on the basis curve c is in the direction - - - - s = v x t where v = c.refDirection() and - t = c.tangent() - For the offset direction to be well-defined, v shall not on any point of the curve be in the same, or opposite, direction as - t. The default value of the refDirection shall be the local co-ordinate axis vector for elevation, which indicates up for the curve in a geographic sense. NOTE! If the refDirection is the positive tangent to the local elevation axis (\"points upward\"), then the offset vector points to the left of the curve when viewed from above.'